좌표하강알고리즘(Coordinate Descent Algorithm, CDA)

0. lm함수의 한계

 R에서 회귀 계수를 추정하는 일은 간단하게 lm함수를 사용하면 가능하다. 하지만, 지난번에 소개했던 4가지 경우 lm함수가 제대로 작동하지 않는다는 문제점이 존재한다. 이를 해결하기 위한 여러 알고리즘 중 좌표하강 알고리즘(이하 CDA)에 대해 소개하도록 하겠다. 

https://mn0317.tistory.com/9

회귀 모형의 벡터와 행렬 표현

lm함수가 잘 작동되지 않는 경우에 대해 알고싶다면 위의 글을 참고하기를 바란다.

 

1. CDA 논리

 CDA의 기본 논리는 다음과 같다. 우리가 추정하는 베타들의 초기값을 설정한 후, 이 초기값들의 좌표를 하나하나 갱신해 나가는 과정이며, 특정한 기준에 수렴할 때까지 갱신을 계속해서 반복하는 과정을 말한다. 여기서 한 좌표의 값이 갱신될 때, 나머지 좌표의 값은 바로 직전에 갱신된 값을 사용한다. 

 

2. CDA 절차

 구체적인 CDA 기호의 표현은 다음과 같다.

이 기호의 뜻은 r번째 반복을 통해 얻어진 j번째 계수의 값을 말한다.

따라서 초기값 설정은 다음과 같이 표현될 수 있다.

이는 0번째 반복, 즉, 초기값의 벡터들을 뜻한다.

반복수 r=1,2,...에 대하여 j=1,...,J순으로 위의 값은 다음과 같이 갱신이 된다. 

 

이는 갱신된 베타의 일반화 된 식이다. 잘 살펴보면 알겠지만, 베타 r번째 반복을 통해 j번째 계수를 구하기 위해 첫 번째 베타부터 j-1번째 베타까지는 r번의 갱신된 값을 사용하였고, j+1부터 J번째까지의 계수들은 모두 r-1번 갱신된 값을 사용하였다. 

즉, 이는 위 식은 베타 j를 구하기 위한 일변량 함수로 변형되는 것을 알 수 있다. 왜냐하면, 베타 j 이전의 값들과 이후의 값들은 각각 r번, r-1번의 반복을 통해 얻은 값들을 사용하였기 때문에, 미지수가 아닌 이미 밝혀진 상수들이기 때문이다.

따라서, 이러한 반복을 많이하면 많이 할수록, CDA에 의하여 갱신된 값은 각각의 베타 값의 최소해로 수렴하는 것을 알 수 있다. 

 

반복수를 무한히 가져가면 잔차제곱합을 최소로하는 beta hat의 값으로 수렴한다.

 예를 들어 단순선형회귀모형에서, 베타1과 베타2를 추정한다고 생각해보자, 초기값은 좌표 (베타1,베타2)=(0,0)으로 설정한다. 첫 번째 시도에서 베타1을 구할 때, 베타2를 0으로 두고, 목적함수 R(베타)(잔차제곱합)를 미분해 최소값을 갖는 베타1을 갱신된 베타1의 값으로 둔다. 그리고 베타2를 구할 때, 갱신된 베타1의 값을 잔차제곱식에 대입하여 또 미분하여 0이 되는 베타 2를 구한다. 다음의 베타 1을 구할 때는 직전에 구한 베타 2의 값을 사용한다. 이렇게 계속 반복해 적절한 베타 값을 찾는 과정이 CDA인 것이다. 

 

시각화 하면 다음과 같이 표현 가능하다. 

위 등고선은 바깥에서 안 쪽으로 올수록 높이(값)가 낮아지는 3차원 그래프이다. 초기값에서 반복해서 갱신할수록, 해당식의 해에 점점 근접하는 것을 알 수 있다.

 

위의 그림을 다르게 표현하면 다음과 같다.

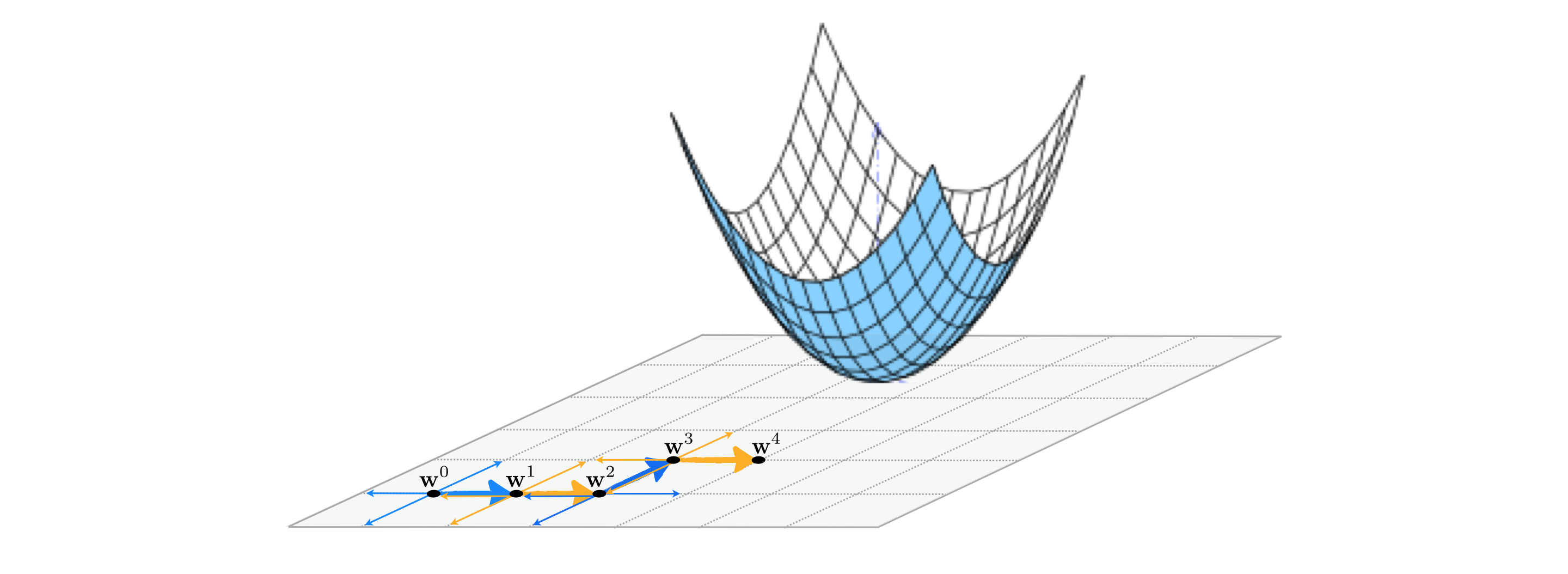
3. r번째 반복에서의 j번째 계수 방정식의 일반화(최소잔차제곱합)

  앞서 말했듯, r번째 반복에서의 j번째 계수를 구하기 위해 그 이전의 계수들은 r번째 반복된 값을, 그 이후의 계수들은 r-1번째 갱신된 값을 사용한다는 것을 알 수 있다. 

 

r번째 반복에서 j번째 계수 = 해당식을 최소화하는 값

이는 결국 위에 나타난 해당식을 beta j에 대한 이차식으로 표현하여 최소값을 계산하는 것이 핵심이다. 중학교 수학에도 나오지만 이차식 ax^2+bx+c의 최소값은 -b/2a에서 발생하는 것을 알 수 있다. 

즉, 다음과 같이 표현가능해야 한다. 

 

해당식을 beta j에 대한 이차식으로 표현하여 해당식을 최소로 만들어주는 beta j의 값을 구한다.

해당식은 결국 잔차제곱합에 위의 계수들을 대입하는 것으로 다음과 같이 나타낼 수 있다.

 

본래 잔차제곱합은 우리가 앞서 다음과 같이 표현했었다. 

 

하지만, 위의 식은 반복수(r)에 따라 갱신된 값이 다르므로 다음과 같이 표현을 바꿀 수 있다. 

베타 j와 Bj의 합을 나머지의 항들과 따로 분리한 식이다.

빨간색으로 표시된 부분은 보면 알겠지만, 1부터 j-1까지의 계수들이 r번째 갱신된 값이 적용되었고, j+1부터 J번째까지의 계수들은 r-1번째 갱신된 값이 적용된 것을 표현한 것이다. 그리고 여기서 beta j는 미지수이며 우리가 구해야 하는 값이다. 

 

여기서 빨간색으로 표시된 부분을 다시 다음과 같이 변형할 수 있다. 

위의 y(r)ij를 부분잔차라고 하며, 보면 알 수 있듯, r번째 반복에서 j번째 기저의 적합을 제외하고 계산된 부분을 말한다.

이를 적용해서 다시 식을 표현하면 다음과 같다. 

이는 r번째 반복에서 j번째 beta의 값을 구하기 위한 최종식이 된다.

결국 beta j의 이차식으로 표현된 것을 확인할 수 있다. 여기서 Bj는 이전 글에서도 설명했듯, 기저함수이므로 우리가 아는 값인 상수이며, 부분잔차에 해당하는 값도 상수이므로 결국 이는 beta j에 대한 이차식이다. 따라서 위 식을 최소값으로 만들어주는 beta j는 다음과 같다. 

최종적으로 나온 r번째 반복에서 j번째 계수의 일반화된 식이다.

 여기서 반복 수를 무한으로 보내주면 기존 베타 hat에 대해 매우 근접한 값을 구할 수 있다. 

반복수를 무한히 가져가면 잔차제곱합을 최소로 만들어주는 beta hat의 값으로 수렴한다.

---

 하지만, 실제 코딩에서는 r을 무한히 돌릴 수 없으므로, 알고리즘을 멈출 수 있는 stopping rule을 설정해 주어야 한다.

우리는 r번째 반복에서 구한 베타 j와 그 이전 반복에서 구한 베타j의 값이 크게 다르지 않으면 멈추는 것으로 코딩을 할 수 있다. 

 식으로 표현하면 다음과 같다. 

 

똑같은 beta j에 대해서 r번째 갱신된 값과 그 이전의 값이 입실론(아주 작은 수)보다 작으면 알고리즘을 멈춘다.

여기서 입실론은 아주 작은 수이며 코딩하는 사람이 설정할 수 있다. 개개인마다 다르지만, 주로 0.00001로 설정한다. 

 

정리하자면 CDA는 다른 방식으로 회귀계수를 구하는 알고리즘이며, 이는 초기값으로부터 좌표들을 계속해서 갱신해 나감으로써 베타 hat을 구하는 과정이다. 또한 이를 구하는 구체적인 식을 살펴보았다. 

 

다음 글에서는 해당 CDA를 R프로그래밍에서 직접 구현해보도록 하겠다.