| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 라쏘회귀
- TRANSFORMER
- self-attention
- transfer learning
- lasso
- CDA
- R
- Cross-Validation
- nlp
- image classification
- 통계학
- attention
- RidgeRegression
- CV
- BERT
- Encoder
- vision transformer
- 좌표하강알고리즘
- Identity mapping
- 릿지회귀
- 선형회귀
- Inductive bias
- Residual learning
- LassoRegression
- RESNET
- rnn
- VIT
- glmnet
- decoder
- Today
- Total
통계 이야기
함수추정에서의 좋은 모형 본문
0. 다양한 함수평활
앞선 글에서 살펴보았듯, 기저함수방법론을 통해 다양한 형태의 함수들을 적합할 수 있었다. 함수의 형태는 스플라인 기저함수들을 차수에 따라, 혹은 매듭점의 위치와 개수에 따라 달라지곤 했는데, 오늘은 이렇게 수많은 함수들 중 좋은 모형은 무엇인지에 대해서 설명해보고자 한다.
1. 매듭점 개수
먼저 매듭점의 개수를 선택하는 방법이다. 보통 데이터를 n개라고 하면, 일단 매듭점의 개수는 n보다는 작아야 할 것이다. 데이터의 개수보다 많은 매듭점을 설정하는 것은 불가능하기 때문이다. 우선 매듭점의 상한선을 정하는데, 보통 데이터의 개수 n에 비례하여 설정한다. 예를 들어 데이터의 10프로, 5프로... 등등. 매듭점의 상한선을 K라고 했을 때, 이 K가 정해졌다면, 매듭점의 개수 1...k... K까지 중에서 최적의 모형을 나타내는 함수를 찾으면 된다.
2. 매듭점의 위치
매듭점의 위치는 크게 두 가지 방법으로 정할 수 있다. 첫번째 방법은 간단하게 x값의 범위에 따라 등간격으로 k만큼 배분하는 것이다. 두 번째 방법으로, 데이터의 분포가 고르지 않고 한 쪽으로 편향되어 있을 경우에는 x값의 범위 내에서 분위수를 정해 k개의 매듭점을 설정할 수 있다.
3. 최적모형 선택 기준
매듭점의 위치와 상한선이 정해졌다면, 다양한 척도들에 의해 좋은 모형을 찾을 수 있다. 크게 3가지 기준들이 존재하는데, 수정된 결정계수, AIC, BIC, 교차타당법이 그것이다.
3.1 수정된 결정계수(Adjusted R-square)
먼저 수정된 결정계수에 대해서 소개해보도록 하겠다. 회귀분석에서 회귀모형에 대한 평가를 할 때, 결정계수(R-square)라는 값이 존재했었다. 이는 모형이 얼마나 잘 적합이 됐는지를 판단할 수 있는 척도였다. 하지만, 여기에는 단점이 존재했는데, 이는 변수의 개수가 많아지면(우리의 경우 매듭점의 개수가 많아지면) 무조건 높은 값이 나오기 때문이다. (결정계수는 적합도에 대한 평가이기 때문에 값이 높을수록 모형의 적합이 잘 된 것으로 판단한다.) 이는 변수의 개수에 대한 고려를 하지 않기 때문인데, 이에 대한 대안으로 나온 것이 바로 수정된 결정계수이다.

수정된 결정계수는 좋은 매듭점(변수)를 추가하면 값이 높아지고, 유용하지 않은 변수(매듭점)을 사용하면 값이 낮아진다는 점에서 그냥 결정계수와 차이가 있다. 정리하자면, 결정계수는 매듭점의 개수가 많아질수록 증가하지만, 수정된 결정계수는 가치있는 매듭점을 설정해야 그 값이 올라간다는 것이다.
따라서 수정된 결정계수가 높은 모형이 무조건적으로 매듭점이 많은 모형이 아니라 가치 있는 매듭점이 있는 모형이라는 뜻이다.

위 그래프에서 x축은 매듭점의 개수 y축은 각각 결정계수와 수정된 결정계수를 나타낸다. 결정계수, 수정된 결정계수 모두 높을수록 좋은 모형이라는 뜻이므로, 가장 높은 값을 확인해보자. 결정계수 같은 경우에는 매듭점의 개수가 가장 많은 30개, 수정된 결정계수 같은 경우에는 매듭점의 개수가 8개로 매듭점의 개수가 훨씬 더 적은 모형을 좋은 모형으로 판단한 것을 알 수 있다.
3.2 AIC(Akaine Information Criterion)와 BIC(Bayes Information Criterion)
AIC와 BIC 모두 편향과 분산의 trade - off 관계를 고려한 지수들이다. 먼저 식을 살펴보면 각각 다음과 같다.
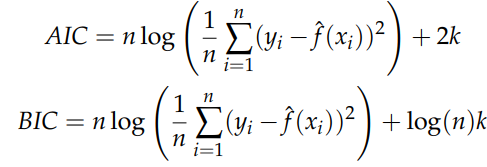
AIC와 BIC 모두 잔차제곱합의 평균에 로그를 취했다. 이는 모형을 얼마나 적합을 잘했는지, 적합도에 관한 내용이며, 뒤의 항은 매듭점의 개수가 많아지면 그 값이 커지도록 하는 패널티 항에 해당한다. 즉, 본래 적합을 잘하기 위해서는 많은 매듭점의 개수가 필요했는데 그렇게 하면 패널티 항의 크기가 커지므로 AIC의 값이 커지게 된다. 우리는 따라서 이 둘의 값의 합이 적절하게 작은 모형을 선택해야 한다. (참고로 위 두 척도는 값이 작을수록 좋은 모형이다.)
BIC는 기본 원리는 AIC와 별 차이가 없으나 다만 패널티 항의 정도가 훨씬 더 크다. 데이터의 개수(n)이 보통 8을 넘어간다면, BIC의 패널티 항이 훨씬 더 민감해질 것이다. 그래서 보통 데이터가 충분히 크다면, AIC보다 BIC가 훨씬 더 간단한 모형을 제안한다.
3.3 교차타당법(Cross-Validation)
교차타당법을 알기 위해서는 먼저 prediction error, test error, training error에 대해서 알아야한다. 그 전에 먼저 교차타당법을 실시할 때 훈련데이터(training data)와 평가 데이터(test data)로 데이터를 분리한다. 보통 비율은 8대 2정도 된다. 먼저 훈련 데이터로 지금까지 소개한 방법으로 모델을 적합한다. 그리고 이 적합한 모델에 평가 데이터를 대입해서 그 결과값이 평가데이터의 반응변수 값과 얼마나 차이가 있는지에 대해서 확인하는 것이 test error인 것이다. 보통 이 차이를 확인할 때는 잔차제곱합의 평균을 계산한다. 이렇게 구한 test error의 평균을 prediction error라고 한다.

위 식에서 yi'과 xi는 각각 테스트 데이터이며, 추정된 함수인 f_hat은 훈련 데이터를 통해 적합된 모형이다. 이에 대한 잔차제곱합의 평균이 test error이다.
그렇다면 우리는 왜 훈련 데이터가 아닌 평가 데이터를 사용하는 것일까? 그 이유는 훈련 데이터를 사용할 경우, 매듭점의 개수가 많아질수록 잔차제곱합이 작아지기 때문이다. 따라서 우리가 원하는 좋은 모형을 제공해주지 못한다.
이제 교차타당법에 대해 본격적으로 설명해보도록 하겠다. 먼저 교차타당법은 앞서 설명했던 것처럼 데이터 셋을 훈련 데이터와 평가 데이터로 나누는데 이 과정을 k번 반복하면, k-folds-cv라고 한다.
예를 들어 우리는 데이터 셋을 다음과 같이 분류할 수 있다.

이렇게 분류한 데이터 셋에서 처음에는 1번이 평가 데이터가 되고 2,3,4,5번이 훈련 데이터가 되어서 각 매듭점의 개수에 따라 각각 함수를 추정한다. 그리고 그렇게 추정된 함수에 1번의 데이터를 넣어서 잔차제곱합을 구한다. 그러면 각 매듭점의 개수에 따라 각각의 test error들이 나온다. 이게 첫번째 반복의 끝이다. 이제 2번이 test data가 되고 그 다음은 3번,... 이렇게 해서 5번 반복하여 나온 각각의 test error들의 평균을 내면 이것이 prediction error에 해당된다. 이렇게 데이터들을 교차 반복시켜 검증한다는 점에서 교차타당법이라 불린다.
다시 함수추정의 문제로 돌아와서, 교차타당법을 진행했을 경우, 매듭점의 개수마다 prediction error들이 존재할 것이다.(매듭점의 개수마다 다른 함수를 추정하므로) 따라서 매듭점의 개수가 늘어날때마다 그에 따른 prediction error을 확인한 후, prediction error을 가장 작게 해주는 매듭점의 개수를 선택한다.
그래프로 보이면 다음과 같다.

위의 그래프를 보면 알 수 있지만, 적당한 매듭점의 개수에서 가장 작은 prediction error을 나타내는 것을 볼 수 있다. 위의 같은 경우에는 매듭점의 개수가 6개인 모형을 선택하는 것이 적절할 것이다.
하지만 추정된 prediction error는 말그대로 추정한 값이기 때문에 그 오차가 존재한다. 따라서 가장 작은 prediction error에 존재하는 오차까지도 고려하는 방법이 있다. 이를 The one standard error rule이라고 한다. One standard error rule은 가장 작은 prediction error에서 1표준오차만큼 더한 값을 가지는 다른 모형들 중 매듭점의 개수가 가장 작은 모형을 선택하는 방법이다.

위 그래프에서 검정색 그래프를 살펴보면, prediction error을 가장 낮게 해주는 매듭점의 개수는 20개에 해당한다. 해당 prediction error에 1표준오차를 더한 값은 노란색 선에 해당하고 이 노란색 선에 해당하는 prediction error을 가지는 매듭점의 개수 중 가장 작은 매듭점의 개수를 선택한다. 그것이 첫번째 초록색 수직선에 해당하는 것이다. 여기서 노란색 선과 검은색 선이 만나는 지점은 다른 곳에서도 발생하는데 첫번째 초록색 수직선을 고르는 이유는 무엇일까? 그 이유는 앞서 설명했던 간명성의 성질 때문이다. 같은 prediction error을 가지는 모형이라면, 가장 간단한 모형을 선택하는 것이 해석하기에도 훨씬 수월하기 때문이다.
4. 요약 및 정리
지금까지 쓴 글을 정리해보자면, 함수추정에서 좋은 모형을 선택하기 위해서는 적절한 매듭점의 개수를 선택해야 하는데, 그것을 판단할 수 있는 방법으로는 크게 3가지가 있었다. 수정된 결정제곱, AIC, BIC, 교차타당법이 그것이었고 이 3가지 모두 데이터에 기반한 의사결정을 할 수 있도록 그 기준을 제시해 준다.
'통계학 > 비모수통계학' 카테고리의 다른 글
| 다양한 스플라인 함수추정 (0) | 2023.06.08 |
|---|---|
| 회귀 스플라인 (0) | 2023.04.18 |
| R에서 CDA를 통해 회귀식 구현하기 (0) | 2023.04.03 |
| 좌표하강알고리즘(Coordinate Descent Algorithm, CDA) (1) | 2023.04.03 |
| 회귀 모형의 벡터와 행렬 표현 (0) | 2023.04.03 |




